mNo edit summary |
No edit summary |
||
| Line 8: | Line 8: | ||
==='''Using [[Circle Inversion]]'''=== |
==='''Using [[Circle Inversion]]'''=== |
||
We can use properties of circle inversion to help us prove Ptolemy's theorem. We won't go over all of them here, but here are the ones relevant to this proof. For simplicity, we'll let all circles be labelled ''O'' and all tangent points be labelled ''T''. If a point is labelled ''A'', its image under inversion is labelled ''A<sub>I</sub>''. |
We can use properties of circle inversion to help us prove Ptolemy's theorem. We won't go over all of them here, but here are the ones relevant to this proof. For simplicity, we'll let all circles be labelled ''O'' and all tangent points be labelled ''T''. If a point is labelled ''A'', its image under inversion is labelled ''A<sub>I</sub>''. |
||
| − | ===='''Overview'''==== |
+ | ===='''Abridged Overview of Circle Inversion'''==== |
| + | [[File:Circle_Inversion.png|thumb|Illustration of circle inversion applied to a point ''A''.]] |
||
| − | |||
The fundamental process of circle inversion is to invert a point ''A'' to its image ''A<sub>I</sub>''. The process is as follows for any point inside the circle: |
The fundamental process of circle inversion is to invert a point ''A'' to its image ''A<sub>I</sub>''. The process is as follows for any point inside the circle: |
||
#Draw a circle ''O''. |
#Draw a circle ''O''. |
||
| Line 24: | Line 24: | ||
#Join ''OT''. This will always be perpendicular to line ''AT''. |
#Join ''OT''. This will always be perpendicular to line ''AT''. |
||
#Draw a line perpendicular to ''OA'' at point ''T'', marking a point ''A<sub>I</sub>'' where the line intersects ray ''OA'', thus making the line ''TA<sub>I</sub>''. |
#Draw a line perpendicular to ''OA'' at point ''T'', marking a point ''A<sub>I</sub>'' where the line intersects ray ''OA'', thus making the line ''TA<sub>I</sub>''. |
||
| + | [[File:Inversion_of_a_Circle_through_the_Center,_Roughly.png|thumb|Inversion of a circle through the center, roughly approximated to illustrate the point.]] |
||
| + | If a circle ''N'' is drawn that passes through the center of circle ''O'', then the circle inverts to a line that does not pass through the center of that circle. Its distance from the center depends on how close circle ''N'' is to the edge of circle ''O''. |
||
| + | ===='''Property I: Scaling of Inverted Points'''==== |
||
| + | Refer to the above constructions. For simplicity, let point ''A'' be inside the circle. |
||
| + | We can observe the following: |
||
| + | :△''OTA'' ~ △''TA<sub>I</sub>A'' ~ △''OA<sub>I</sub>T'' |
||
| + | The three triangles share the same angles, thus they are all similar. We shall refer to △''OTA'' and △''OA<sub>I</sub>T''. Since they're similar, we can deduce the following: |
||
| + | :''OT'' ~ ''OA<sub>I</sub>'', and ''OA'' ~ ''OT''. |
||
| + | :<math>\therefore \frac{OT}{OA_{I}} = \frac{OA}{OT}</math> |
||
| + | Multiplying both sides by ''OA<sub>I</sub>'' and ''OT'' gives us the following: |
||
| + | :''OT''<sup>2</sup> = ''OA'' × ''OA<sub>I</sub>''. |
||
| + | Since ''OT'' will always be the radius of the circle, let's refer to this line as ''r''. |
||
| + | Therefore, ''OA'' × ''OA<sub>I</sub>'' = ''r''<sup>2</sup>. |
||
| + | ===='''Property II: Scaling of Inverted Segments'''==== |
||
| + | Now that we have obtained the scaling of points, let's focus on the scaling of inverted segments. For simplicity, we will not draw the circle of inversion here. |
||
| + | [[File:Inverted_Segment.png|thumb|Reference figure for this section.]] |
||
| + | In the provided figure, we see two triangles: △''OAB'' and △''OA<sub>I</sub>B<sub>I</sub>''. |
||
| + | We can observe the following: |
||
| + | :△''OAB'' ~ △''OB<sub>I</sub>A<sub>I</sub>'' |
||
| + | Both triangles share a common angle α from ''O'', and both sides scale to give us ''r''<sup>2</sup>, as shown in the previous section. We can therefore deduce the following: |
||
| + | :''OA'' × ''OA<sub>I</sub>'' = ''OB'' × ''OB<sub>I</sub>'' |
||
| + | :<math>\therefore \frac{OA}{OB} = \frac{OA_{I}}{OB_{I}}</math> |
||
===='''Application'''==== |
===='''Application'''==== |
||
==Corollaries== |
==Corollaries== |
||
Revision as of 02:34, 4 August 2020
In Euclidean geometry, Ptolemy's theorem regards the edges of any quadrilateral inscribed within a circle.
Ptolemy's theorem states the following, given the vertices of a quadrilateral are A, B, C, and D in that order:
If a quadrilateral can be inscribed within a circle, then the product of the lengths of its diagonals is equal to the sum of the products of the lengths of the pairs of opposite sides.
Proofs
Using Circle Inversion
We can use properties of circle inversion to help us prove Ptolemy's theorem. We won't go over all of them here, but here are the ones relevant to this proof. For simplicity, we'll let all circles be labelled O and all tangent points be labelled T. If a point is labelled A, its image under inversion is labelled AI.
Abridged Overview of Circle Inversion

Illustration of circle inversion applied to a point A.
The fundamental process of circle inversion is to invert a point A to its image AI. The process is as follows for any point inside the circle:
- Draw a circle O.
- Draw a point A anywhere inside the circle.
- Draw a ray OA.
- Draw a line perpendicular to OA, marking a point T where the line intersects the circle, thus making the line AT.
- Join OT.
- Draw a line perpendicular to OT at point T, marking a point AI where the line intersects ray OA, thus making the line TAI. This is a tangent of circle O.
For any point outside of the circle:
- Draw a circle O.
- Draw a point A anywhere inside the circle.
- Draw a ray OA.
- Draw a line at A, marking a point T where the line intersects the circle, thus making the line AT. This is a tangent of circle O.
- Join OT. This will always be perpendicular to line AT.
- Draw a line perpendicular to OA at point T, marking a point AI where the line intersects ray OA, thus making the line TAI.

Inversion of a circle through the center, roughly approximated to illustrate the point.
If a circle N is drawn that passes through the center of circle O, then the circle inverts to a line that does not pass through the center of that circle. Its distance from the center depends on how close circle N is to the edge of circle O.
Property I: Scaling of Inverted Points
Refer to the above constructions. For simplicity, let point A be inside the circle.
We can observe the following:
- △OTA ~ △TAIA ~ △OAIT
The three triangles share the same angles, thus they are all similar. We shall refer to △OTA and △OAIT. Since they're similar, we can deduce the following:
- OT ~ OAI, and OA ~ OT.
Multiplying both sides by OAI and OT gives us the following:
- OT2 = OA × OAI.
Since OT will always be the radius of the circle, let's refer to this line as r. Therefore, OA × OAI = r2.
Property II: Scaling of Inverted Segments
Now that we have obtained the scaling of points, let's focus on the scaling of inverted segments. For simplicity, we will not draw the circle of inversion here.
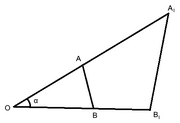
Reference figure for this section.
In the provided figure, we see two triangles: △OAB and △OAIBI.
We can observe the following:
- △OAB ~ △OBIAI
Both triangles share a common angle α from O, and both sides scale to give us r2, as shown in the previous section. We can therefore deduce the following:
- OA × OAI = OB × OBI
Application
Corollaries
Pythagorean Theorem
If the quadrilateral is a rectangle or a square, then Ptolemy's theorem can be used to prove the Pythagorean theorem.
Since the shape is a rectangle or a square, then each side is congruent to its opposite, as are the two diagonals. Given the vertices of a quadrilateral are A, B, C, and D in that order:
Let's designate the letters a, b, and c to each of these pairs.
Let's substitute each of these values in the formula for Ptolemy's theorem. This gives us the following:








